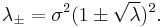Marchenko–Pastur distribution
In random matrix theory, the Marchenko–Pastur distribution, or Marchenko–Pastur law, describes the asymptotic behavior of singular values of large rectangular random matrices. The theorem is named after Ukrainian mathematicians Vladimir Marchenko and Leonid Pastur who proved this result in 1967.
If  denotes a
denotes a 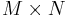 random matrix whose entries are independent identically distributed random variables with mean 0 and variance
random matrix whose entries are independent identically distributed random variables with mean 0 and variance 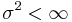 , let
, let
and let 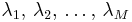 be the eigenvalues of
be the eigenvalues of 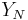 (viewed as random numbers). Finally, consider the random measure
(viewed as random numbers). Finally, consider the random measure
Theorem. Assume that 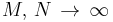 so that the ratio
so that the ratio 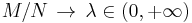 . Then
. Then  (in weak* topology in distribution), where
(in weak* topology in distribution), where
and
with
The Marchenko–Pastur law also arises as the free Poisson law in free probability theory, having rate  and jump size
and jump size  .
.
See also
References
- Götze, F and Tikhomirov, A. (2004) "Rate of convergence in probability to the Marchenko–Pastur law", Bernoulli, 10 (3), 503–548. doi:10.3150/bj/1089206408
- Marchenko,V. A., Pastur, L. A. (1967) "Distribution of eigenvalues for some sets of random matrices", Mat. Sb. (N.S.), 72(114):4, 507–536 doi:10.1070/SM1967v001n04ABEH001994 Link to free-access pdf of Russian version
- Nica, A.; Speicher, R. (2006) Lectures on the Combinatorics of Free probability theory, Cambridge Univ. Press ISBN 0-521-85852-6 (pp. 204, 368). Link to free download Another free access site
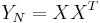
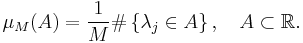
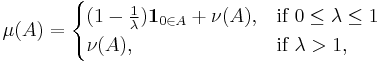
![d\nu(x) = \frac{1}{2\pi \sigma^2 } \frac{\sqrt{(\lambda_{%2B} - x)(x - \lambda_{-})}}{\lambda x} \,\mathbf{1}_{[\lambda_{-}, \lambda_{%2B}]}\, dx](/2012-wikipedia_en_all_nopic_01_2012/I/973153c718ca5043c47dbb611dd887b9.png)